چند ضلعی ها

  چند ضلعی ها
تعریف چند ضلعی :
هر خط شکسته بسته را چند ضلعی می نامند . مثلث یک چند ضلعی (سه ضلعی) است. اگر یکی از زوایای داخلی چند ضلعی بزرگتراز 180 درجه باشد،چند ضلعی را مقعر و در غیر این صورت چند ضلعی را محدب می نامند.

برای دیدن مطالب به ادامه مطلب مراجعه کنید .

---

   
تعریف چند ضلعی :
هر خط شکسته بسته را چند ضلعی می نامند . مثلث یک چند ضلعی (سه ضلعی) است. اگر یکی از زوایای داخلی چند ضلعی بزرگتراز 180 درجه باشد،چند ضلعی را مقعر و در غیر این صورت چند ضلعی را محدب می نامند.

چندضلعی محدب   کوژ:

به چندضلعی گفته می شود که اندازه ی هر زاویه ی آن از  180درجه کم تر باشد،چند ضلعی کوژ یک چند ضلعی ساده‌است که سطح آن یک مجموعه محدب را تشکیل دهد،( رسم یک پاره خط درون شکل) به عبارت دیگر باید بتوان از هر دو نقطه داخل چندضلعی خطی بین آن دو نقطه کشید در حالیکه تمام آن پاره خط درون چند ضلعی قرار داشته باشد.

مانند متوازی الاضلاع ، لوزی ، ذوزنقه و...

چندضلعی کوژ دارای دو ویژگی مهم زیر است:

• هر زاویه داخلی این نوع چندضلعی‌ها باید کمتر یا مساوی ۱۸۰ درجه باشد.
• خط واصل بین هر دو نقطه دلخواه داخل یا روی چندضلعی کاملا داخل یل روی چندضلعی قرار داشته باشد.
• 
  

چند ضلعی کاو یک چند ضلعی ساده است که کوژ(محدب) نباشد ، به عبارت دیگر یک مجموعه محدب را تشکیل ندهد.

ویژگی های چند ضلعی کاو

• حداقل یکی از زاویه های داخلی این نوع چند ضلعی بیشتر از ۱۸۰ درجه است.
• خط واصل بین دو نقطه دلخواه از داخل چند ضلعی لزوما به طور کامل داخل چند ضلعی قرار نمی گیرد

یک چند ضلعی کاو قابل قسمت به دو یا چند چند ضلعی کوژ است.

ویک ضلع آن چند تا  ضلع درون شکل ادامه می یابد. مثل: شکل یک ستاره چند پر

قطر در چند ضلعی های کاو با همان فرمول   2÷(n)(n-3)= تعدادقطر  انجام می شود.جالب: اما تعدادی از قطر ها

در خارج چند ضلعی کاو تشکیل می شود.

    قطر ها در 5 ضلعی کاو

مجموع اندازه های زوایای هر n ضلعی برابر با=180×(2-n)درجه است.
برای مثال ، مجموع اندازه های زوایای یک هفت ضلعی برابر با

900=180×(7-2)درجه است.  

 تعداد قطرهای هر n ضلعی محدب(کاو) برابر با ½ (n)(n-3)= تعدادقطر  است و همگی در داخل شکل رسم می شوند.

½ (n)(n-3)= تعدادقطر

چند ضلعیهای منتظم یعنی  اندازه زاویه با هم ، اندازه ضلعها باهم مساویند. با افزایش تعدا ضلعها شکل تبدیل به دایره شد.

در چند ضلعیهای منتظم با تعداداضلاع زوج، اضلاع مقابل  هم ، با هم موازیند 

  در هر چند ضلعی منتظم با تعداد اضلاع فرد، عمودمنصف هر ضلع ، نیمساز زاویه مقابل به آن ضلع است. که این عمود منصف (یا نیمساز) محور تقارن آن چند ضلعی است.

ویژگیهای متوازی الاضلاع

الف) در هر متوازی الاضلاع، اضلاع مقابل با هم برابر هستند.

ب)درهر متوازی الاضلاع زاویه های مقابل برابرند و هر دو زاویه مجاور یک ضلع مکمل یکدیگرند. همچنین مجموع دو زاویه مجاور برابر 180 درجه است.

ج) در هر متوازی الاضلاع قطرها منصف یکدیگرند.

د) در هر متوازی الاضلاع نقطه تقاطع دو قطر مرکز تقارن آن شکل است.

ه‍) مساحت متوازی الاضلاع برابر با حاصلضرب قاعده در ارتفاع وارد بر آن است.

ز) در هر متوازی الاضلاع، نیمسازهای داخلی دو به دو بر هم عمودند

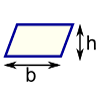Tمساحت متوازی الاضلاع=قاعده ×ارتفاع: مساحت = b × h (h  = ارتفاع                قاعده = b  )

لوزی

لوزی متوازی الاضلاعی است که چهار ضلع آن با هم برابر باشند. بنابراین لوزی کلیه ویژگیهای متوازی الاضلاع را دارد.

مساحت و محیط لوزی :
مساحت لوزی برابر نصف حاصلضرب اندازه های دو قطر است.

نکته 1 :
از هر لوزی یک دایره محاطی می گذرد

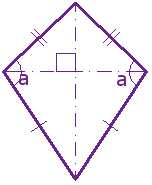
کایت یا شبه لوزی ، چهار ضلعی محدبی است که دارای دو جفت اضلاع مجاور مساوی با دو اندازه مختلف باشد. در واقع کایت چهار ضلعی محدبی است که دارای دو قطر عمود بر هم باشد و فقط یکی از قطرها منصف قطر دیگر باشد. قطری که منصف قطر دیگر است، محور تقارن کایت و همچنین نیمساز دو زاویه مقابل است. مساحت کایت مانند مساحت لوزی محاسبه می شود.

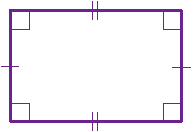
مستطیل متوازی الاضلاعی است که یک زاویه آن قائمه باشد. بنابراین مستطیل کلیه ویژگیهای متوازی الاضلاع را داراست. خطی که وسط دو ضلع مقابل را به هم وصل کند محور تقارن مستطیل است. بنابراین مستطیل دو محور تقارن دارد.

نکته 1 :
مساحت مستطیل برابر حاصلضرب طول در عرض آن است.

دوقطر مساوی دارد که در وسط همدیگر را قطع کردند.,  .

اندازه قطر= ریشه دوم (مجذور طول + مجذورعرض): قطر= "d" = √(w2 + h2)

نکته 2 :
بر مستطیل یک دایره محیطی می گذرد.

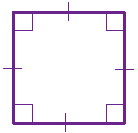
مربع مستطیلی است که چهار ضلع آن با هم مساوی باشد و یا می توان گفت ، مربع لوزی است که یک زاویه آن قائمه باشد. بنابراین مربع کلیه ویژگیهای متوازی الاضلاع، مستطیل و لوزی را دارد.

مساحت مربع

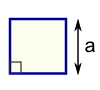مجذور یک ضلع: مساحت = a2 = a × a

مساحت مربع ازراه محاسبه قطر=مجذورقطر÷2: مساحت = d2/2

محاسبه قطر مربع=ضلع × 2√: قطر= "d" = a × √2

مثال: مربع به ضلع5 m, قطر مربع چقدر?

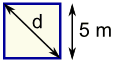طول قطر= a × √2 = 5 × 1.41421... = 7.071 m (با 3 رقم اعشار)

نکته 1 :
در هر مربع قطرها بر هم عمود و با هم برابر و هر کدام محور تقارن شکل هستند.

نکته 2 :
مربع چهار محور تقارن (به تعداد اضلاع) دارد. مربع یک چهار ضلعی منتظم است و کلید ویژگیهای چند ضلعی منتظم را داراست.
مساحت و محیط مربع : مساحت مربع برابر مجذور یک ضلع است.

ذوزنقه

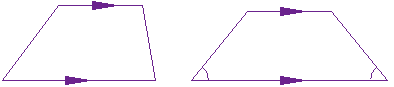
هر چهار ضلعی که فقط دو ضلع آن با هم موازی باشند، ذوزنقه نامیده می شود. دو ضلع موازی را قاعده ها، و دو ضلع غیرموازی را ساقها می نامند. اگر دو ساق ذوزنقه با هم مساوی باشند ذوزنقه را متساوی الساقین می نامند، اگر یکی از ساقها بر دو قاعده عمود باشد ذوزنقه را قائم الزاویه می نامند.

در هر ذوزنقه دو زاویه مجاوز بر هر ساق مکمل یکدیگرند.

نکته 2 :
در هر ذوزنقه متساوی الساقین دو قطر با هم و همچنین دو زاویه مجاور به هر قاعده با هم برابر هستند.

نکته 3 :
پاره خطی که دو سر آن وسط های دو ساق ذوزنقه باشد، موازی دو قاعده آن ذوزنقه و اندازه آن برابر نصف مجموع اندازه های دو قاعده ذوزنقه است.

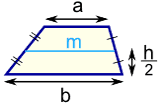
	m =	a+b
		2

مساحت ذوزنقه :
مساحت ذوزنقه با نصف حاصلضرب مجموع دو قاعده درارتفاع آن برابر است.
چهار ضلعی های محیطی


چهار ضلعی محیطی چهار ضلعی است که اضلاع آن بر یک دایره مماس باشند.
درهر چهار ضلعی محیطی مجموع دو ضلع مقابل با مجموع دو ضلع مقابل دیگر برابر است.


چهارضلعی های محاطی
چهار ضلعی محاطی چهار ضلعی است که رأسهای آن بر یک دایره واقع باشد.

نکته 1 :
در هر چهار ضلعی محاطی مجموع دو زاویه مقابل 180 درجه است.

اگرشکل3گوشه وسه ضلع داشت مثلث نام دارد . محدب هستند.	شکلهایی که 4 ضلع و4گوشه دارند را 4 ضلعی گویند. شکل سبز  چند ضلعی کاو است.
5ضلعی 5 گوشه و5ضلع دارد شکل سبز رنگ مقعر است.	6ضلعی 6 گوشه و5ضلع دارد شکل سبز رنگ مقعر است.
چند ضلعی های دیگر :7 ضلعی - 8 ضلعی شباهتها تفاوتهارا در شکلهای زیر بیان کن.

a.	b.  ____________________________________
c. ____________________________________	d. ____________________________________